Introdução
Olá, estudante!
A cinemática dos fluidos trata da descrição do movimento dos fluidos sem, necessariamente, considerar as forças e os momentos que o causam. Introduziremos, aqui, vários conceitos cinemáticos relacionados aos fluidos que fluem. O derivado material (substancial) e seu papel na transformação das equações de conservação com base na descrição lagrangiana de fluxo de fluido (seguindo uma partícula de fluido) ou a descrição euleriana de fluxo de fluido (pertencente a um campo de fluxo).
Também veremos equações comumente usadas na mecânica de fluidos, com uma visão geral dos princípios de conservação e a relação de conservação da massa. Segue-se uma discussão sobre as várias formas de energia mecânica e a eficiência de alguns dispositivos que realizam trabalho mecânico. Continuamos com o desenvolvimento da equação da energia em uma forma adequada para o uso em mecânica dos fluidos, e, ainda, introduziremos o conceito de perda de carga.
Veja, são muitos os estudos que serão abordados aqui, preparado(a) para conhecer um pouco mais sobre cada um deles? Então, vamos lá!
Cinemática dos Fluidos — Velocidade e Aceleração
A cinemática é a parte da mecânica responsável por descrever o movimento. A maneira mais comum de retratar o movimento de um ponto material na mecânica clássica, é usando um vetor de posição \(x\). Esse vetor representa o deslocamento do ponto material em função do tempo \(t\), o que equivale a definir a trajetória descrita pelo ponto material. Se quiséssemos usar esse procedimento retratar o movimento de um fluido, teríamos de ser capazes de dar o vetor posição de cada uma das infinitas partículas de fluido que formam o fluxo.

Fonte: turtlehawk12/ 123RF.
Descrição da figura: A imagem apresenta uma fotografia, nela, vemos uma corrente de água cristalina advinda de um rio em uma pequena queda. No fundo, enxergamos folhagens borradas.
Uma maneira de fazer isso é identificar todas as partículas pela posição \({{x}_{0}}\) que elas ocupam em um instante inicial arbitrariamente escolhido e, em seguida, dar o vetor de posição de todas elas em função dessa posição inicial e tempo:
\[x=x\left( {{x}_{0}},t \right)\]
Os fluidos apresentam movimentos moleculares, ou seja, as moléculas do fluido sempre estão se movimentando de um ponto para outro ponto. Uma porção típica de fluido contém tantas moléculas que ficaria totalmente inviável descrever o movimento de todas as moléculas individualmente (MUNSON; YONG; OKIIDHI, 2004, p. 145).
A velocidade \(v\) e a aceleração \(a\) do ponto material ou da partícula fluida são vetores que podem ser obtidos a partir das derivadas temporais de \(x\):
\[v=\frac{\partial x}{\partial t};~a=\frac{{{\partial }^{2}}x}{\partial t}\]
Dessa forma, estamos descrevendo o movimento do fluido em termos de pontos materiais (ou partículas de fluido), dando sua posição, velocidade e aceleração em função do tempo e de sua posição inicial.
Métodos de análise de fluxo de fluidos — sistemas e volume de controle
Como uma operação unitária dentro da engenharia de alimentos, o transporte de fluidos através de dutos e de tubulações é de grande importância em muitos processos industriais. No estudo do transporte de fluidos, é necessário conhecer, inicialmente, que tipo de fluido é, isso, de acordo com seu comportamento sob a ação de pressões externas.
Quando o volume do fluido é independente de sua pressão e sua temperatura, é um fluido incompressível; pelo contrário, se seu volume varia, o fluido é compressível. Na realidade, nenhum fluido é incompressível, embora os líquidos possam ser assim considerados. Ao contrário, em gases, há uma grande variação de compressibilidade com a pressão e a temperatura.
De acordo com os efeitos produzidos pelas tensões de cisalhamento em um fluido, eles podem ser classificados como newtonianos e não newtonianos, dependendo se seguem ou não a lei de Newton da viscosidade, que determina o tipo de perfil de velocidade do fluido dentro de tubos. Diferentes partes de um fluido em movimento têm distintas velocidades e acelerações. Então, o campo de movimento deve ser descrito em termos de velocidade e de aceleração das partículas.
Existem dois métodos para descrever o movimento de um grupo de partículas em um meio contínuo: Lagrange e Euler. A diferença entre os dois métodos é que, em Lagrange, as coordenadas das partículas são representadas em função do tempo, enquanto, em Euler, são as velocidades das partículas em cada ponto que são dadas em função do tempo.
Geralmente, o engenheiro precisa das informações oferecidas pela análise de Euler, pela qual chegamos a equações integrais de movimento, dentro do chamado volume de controle.
Método Lagrange
O método de Lagrange é uma generalização direta da mecânica do ponto material. Um pequeno volume de fluido é estudado e o movimento de cada uma das partículas é seguido (de coordenadas \(x,~y,~z\)) em função do tempo \(t\), através da equação que descreve a trajetória de cada uma delas. No método de Lagrange, as coordenadas das partículas em movimento são representadas como uma função de tempo. Portanto, ele consiste em acompanhar o movimento de cada partícula fluida, análoga a como é feito na Mecânica dos Sólidos Rígidos.
As leis de Newton são usadas para descrever o movimento desses objetos, e podemos prever com exatidão aonde eles vão e como o momento e a energia cinética são trocados de um objeto para outro. A cinemática dessas experiências envolve acompanhar o vetor posição de cada objeto e o vetor velocidade de cada objeto, como funções do tempo. Quando esse método é aplicado ao escoamento de um fluido, ele é chamado de descrição lagrangiana do momento do fluido em homenagem ao matemático italiano Joseph Louis Lagrange (1736-1813). A análise lagrangiana é análoga à análise de sistemas termodinâmicos; ou seja, seguimos uma massa de identidade fixa (ÇENGEL; BOLES, 2015, p. 104).
Nesse método, as coordenadas de um ponto \(M\) da massa de fluido são uma função do tempo e de sua posição inicial.
\[x={{f}_{x}}\left( {{x}_{0}},{{y}_{0}},{{z}_{0}},t \right)\]
\[y={{f}_{y}}\left( {{x}_{0}},{{y}_{0}},{{z}_{0}},t \right)\]
\[z={{f}_{z}}\left( {{x}_{0}},{{y}_{0}},{{z}_{0}},t \right)\]
Quando consideramos as partículas de um meio contínuo, a abordagem Lagrangiana torna-se extremamente incômoda, uma vez que, a descrição do campo de fluxo requer três vezes o número de parâmetros usados nas equações acima.
Além disso, devido à natureza deformável do meio fluido, geralmente, não é de interesse a história detalhada de uma partícula individual, mas, sim, a inter-relação das propriedades de fluxo em pontos individuais no campo. A principal desvantagem desse sistema é que ainda falta um grande número de equações para descrever o movimento do sistema, então, na prática, não é útil.
Método de Euler
Na aproximação de Euler, desistimos de descrever o movimento do fluido pela densidade \(\rho \left( x,~y,~z \right)\) e pela velocidade \(\underset{\scriptscriptstyle-}{v}\left( \underset{\scriptscriptstyle-}{r},t \right)\) de suas partículas naquele ponto, em função do tempo e do espaço.
Em outras palavras, nesse método, estudamos um ponto no espaço, e como é o movimento do fluido nesse ponto ou em função do tempo.
Segundo Çengel e Boles (2015), na descrição euleriana do escoamento de fluidos, um volume finito chamado de domínio de escoamento ou volume de controle é definido, e é através dele que o fluido escoa para dentro e para fora.
As ferramentas de trabalho são as típicas da teoria de campos, com um campo de pressões, um de velocidades e um de densidades. Será determinada, em função do tempo, a velocidade das partículas do fluido que passam, sucessivamente, por esse ponto. A velocidade será dada por seus três componentes:
\[u={{f}_{u}}\left( x,~y,~z,t \right)\]
\[v={{f}_{v}}\left( x,~y,~z,t \right)\]
\[w={{f}_{w}}\left( x,~y,~z,~t \right)\]
As descrições lagrangianas e eulerianas do mesmo fluxo não são idênticas, pois a velocidade medida em um ponto fixo não se refere a uma única partícula de fluido, mas mede a velocidades das diferentes partículas de fluido que, ao longo do tempo, fluem por esse ponto.
FIQUE POR DENTRO
Lagrange e Euler
No método de Lagrange, as coordenadas das partículas em movimento são representadas em função do tempo. Consiste em acompanhar o movimento de cada partícula de fluido, de forma análoga a como é feito na Mecânica do Sólido Rígido. Nesse método, as coordenadas de um ponto M da massa fluido são uma função do tempo e de sua posição inicial. Já o método de Euler fundamenta-se em considerar um ponto fixo no espaço e estudar, em função do tempo, o que acontece naquele momento. Será determinada, em função do tempo, a velocidade das partículas de fluido que passarem, sucessivamente, por esse ponto.
Fique por dentro, lendo o artigo Uma formulação explícita para a solução de escoamentos em águas rasas, de Martinez e Santos (1999).
Clique no link a seguir: https://bit.ly/3BSSqQr. Acesso em: 6 dez. 2022.
Fonte: Elaborado pela autora.
Quando a descrição euleriana é usada, costumava-se tomar como variável fundamental a posição das partículas do fluido, mais a velocidade medida \(\underset{\scriptscriptstyle-}{v}\) em pontos fixos \(\underset{\scriptscriptstyle-}{x}\) do referencial ao longo do tempo \(t\).
Teorema de transporte de Reynolds
A natureza do fluxo laminar ou turbulento é definida pelo número de Reynolds. Em 1883, o pesquisador Osborne Reynolds estudou o movimento de um fluido. Usando as equações diferenciais gerais que descrevem o fluxo, ele deduziu as condições para que dois fluxos sejam dinamicamente semelhantes, definindo que o grupo adimensional \(''VLr/m''\) deveria ser o mesmo para ambos os casos; por ele, esse parâmetro é conhecido como o número de Reynolds \(Re\).
\[Re=\frac{\rho VD}{\mu }\]
Onde,
\(V\) é uma característica do escoamento que, no caso de tubulações, é a velocidade média \(V\).
\(D~\acute{e}\) um comprimento característico do ambiente ao redor do fluido. Em tubos, geralmente, é o diâmetro.
\(r\) é a densidade do fluido.
\(\rho \) é a massa específica do fluido.
\(\mu \) é o coeficiente de viscosidade do fluido.
Assim, estabeleceram-se alguns parâmetros para o número de Reynolds:
- Re 2100: fluxo laminar. As forças viscosas predominam. A lei de Newton da viscosidade é válida.
- Re 4000: fluxo turbulento. As forças viscosas são quase anuladas devido à turbulência. A lei da viscosidade de Newton é inválida.
- 2100< Re <4000: o fluxo é indeterminado, podendo se comportar como laminar ou turbulento, dependendo das condições circundantes, variando de momentos para outros. É um intervalo em que não se deve trabalhar.
Sobre a temática, Fox, Mcdonald e Pritchard (2014) ressaltam que:
Se o número de Reynolds for “grande”, os efeitos viscosos serão desprezíveis pelo menos na maior parte do escoamento; se o número de Reynolds for pequeno, os efeitos viscosos serão dominantes. Finalmente, se o número de Reynolds não for nem pequeno nem grande, nenhuma conclusão geral poderá ser tirada (FOX; MCDONALD; PRITCHARD, 2014, p. 62).
Para determinar o significado do grupo adimensional, Reynolds realizou seus experimentos com um fluxo de água através de tubos de vidro, para tanto, ele organizou um tubo horizontal com uma extremidade alargada em um reservatório e outra terminada em uma válvula reguladora de fluxo.
Dentro do tubo de ensaio, ele injetou um corante e observou que, para taxas de fluxo e pequenas velocidades e, portanto, baixo número de Reynolds, o filete colorido se moveu traçando uma linha reta sem se misturar com a água circundante, ou seja, o fluxo era laminar. À medida que a vazão e, por consequência, a velocidade, aumentavam, o número de Reynolds subia, até que atingiu uma condição em que a linha era ondulada, chegando ao momento em que se rompeu abruptamente, difundindo-se pelo tubo, ou seja, o regime turbulento.
Osborne Reynolds foi quem primeiro estudou quantitativamente a ocorrência dos escoamentos laminar e turbulento. Ele observou que o escoamento no interior de um duto de seção circular de diâmetro constante é laminar ou turbulento em função de uma relação entre a velocidade de escoamento, o diâmetro interno do duto, a massa específica e a viscosidade dinâmica do fluido. Essa relação, que é adimensional, chamada de número de Reynolds (LIVI, 2017, p. 69).
Começando com o fluxo turbulento no tubo de vidro, Reynolds descobriu que ele sempre se tornará laminar quando desacelerado para tornar-se menor que 2100. Isso é chamado de número de Reynolds crítico inferior para fluxos em tubos e é importante em cálculos práticos. Da mesma forma, ao aumentar o fluxo de laminar a turbulento, observou que para Re maior que 4000, era turbulento. Isso é chamado de número de Reynolds crítico superior. Se o número de Reynolds for menor que 2100, o regime é laminar. Do ponto de vista qualitativo, pode-se dizer que, aumentando o número de Reynolds, de valores inferiores ao indicado como valor crítico (2100), o perfil parabólico de velocidades típicas do fluxo laminar, ele se achata progressivamente, tornando-se uma superfície praticamente plana, perpendicular às paredes.
Se o Reynolds for maior que 4000, a lei da viscosidade de Newton não se aplica mais, impossibilitando resolver analiticamente os perfis de velocidade. À medida que a velocidade aumenta, o movimento de um fluido, que ocorre de forma caótica, em que as partículas se movem desordenadamente e as suas trajetórias se encontram, formando pequenos redemoinhos aperiódicos, como água em um canal de grande pendente, cresce. Assim, pode-se considerar que o perfil de velocidade é praticamente plano, ou seja, as velocidades pontuais são semelhantes entre si e praticamente iguais à média.
Descrição e classificação dos movimentos dos fluidos
A dinâmica dos fluidos estuda líquidos e gases em movimento. Caracterizamos o movimento do fluido por um campo vetorial de velocidades correspondentes à velocidade que cada partícula do fluido possui em cada ponto do espaço que ocupa, e, também, por um campo de pressão escalar referido apenas para os pontos dele.
Um fluido pode fluir em dois tipos de regime:
Considere, para o seu estudo, que os fluidos são divididos em camadas e que elas podem ter várias velocidades, de camada para camada, mas todas as partículas de uma mesma camada ou folha terão sempre a mesma velocidade, independentemente do tempo decorrido durante o seu movimento. Por essa razão, esse regime é considerado estacionário.
Afirma que, em cada ponto do espaço ocupado pelo fluido, a velocidade da partícula que nele é encontrado leva mais de um valor conforme o tempo passa, e, em sua corrente, há formação de redemoinhos.
Para White (2010), na área de fluidos, o primeiro passo de um engenheiro especializado é estimar o intervalo do número de Reynolds do escoamento que está sendo estudado.
Para entender o movimento dos fluidos, é necessário conhecer dois conceitos básicos: linhas de corrente e tubo de corrente. A primeira se refere às linhas em que todos os seus pontos coincidem com o vetor de trajetória da velocidade do fluido em movimento. Enquanto o tubo de corrente é o espaço limitado pelas linhas de fluxo. As partículas de dentro de um tubo de corrente não podem sair, assim como as externas não podem entrar.
O fluxo também é classificado como uni, bi ou tridimensional, dependendo do número de coordenadas espaciais necessárias para especificar o campo de velocidade. Para fins de análise de fluxo de fluido, muitas vezes, é conveniente classificá-los, ainda, de acordo com a velocidade do fluxo. Veja no infográfico a seguir outras classificações relevantes dos fluxos dos fluidos:

É aquele em que as variações de velocidade, de pressão etc., são transversais à direção do fluxo principal. Tem lugar quando a velocidade é a mesma em todos os pontos do fluido em uma seção reta do condutor. A análise unidimensional serve para fornecer soluções aproximadas adequadas em muitos problemas encontrados em engenharia, por exemplo, para caracterizar o escoamento através de um tubo.

Nesse tipo de escoamento, assume-se que todas as partículas seguem trajetórias idênticas em planos paralelos. Não há mudanças nas variáveis do fluxo na direção normal aos referidos planos. Eles são estudados em duas dimensões, por exemplo, o estudo de aterros sanitários e portões.

É o escoamento mais geral, no qual os componentes da velocidade em direções perpendiculares entre si são funções das coordenadas do espaço e do tempo. Exemplos: tubos, curvas, cotovelos, escoamento pelo interior de bombas e turbinas. O campo de velocidades é uma função das três coordenadas do espaço e do tempo.

O vetor velocidade varia em um dado instante de um ponto a outro. Exemplo: Líquido fluindo através de um tubo de seção.

A velocidade em qualquer ponto é constante no tempo. A velocidade de sucessivas partículas que ocupam um ponto nos instantes sucessivos é o mesmo. Essa continuidade no tempo em um ponto pode ser aplicada também ao resto das variáveis que definem o estado do fluido naquele ponto. Exemplo: bombear água através de uma tubulação de fluxo constante.

Quando as condições em um ponto mudam com o tempo, por exemplo, o bombeamento de água em uma tubulação com vazão crescente.
Descrição: há um infográfico interativo que possui seis botões dispostos verticalmente um abaixo do outro, ao clicar em cada um deles, temos: 1. Escoamento unidimensional: é aquele em que as variações de velocidade, de pressão etc., são transversais à direção do fluxo principal. Tem lugar quando a velocidade é a mesma em todos os pontos do fluido em uma seção reta do condutor. A análise unidimensional serve para fornecer soluções aproximadas adequadas em muitos problemas encontrados em engenharia, por exemplo, para caracterizar o escoamento através de um tubo. 2. Escoamento bidimensional: nesse tipo de escoamento, assume-se que todas as partículas seguem trajetórias idênticas em planos paralelos. Não há mudanças nas variáveis do fluxo na direção normal aos referidos planos. Eles são estudados em duas dimensões, por exemplo, o estudo de aterros sanitários e portões. 3. Escoamento tridimensional: é o escoamento mais geral, no qual os componentes da velocidade em direções perpendiculares entre si são funções das coordenadas do espaço e do tempo. Exemplos: tubos, curvas, cotovelos, escoamento pelo interior de bombas e turbinas. O campo de velocidades é uma função das três coordenadas do espaço e do tempo. 4. Escoamento não uniforme: o vetor velocidade varia em um dado instante de um ponto a outro. Exemplo: Líquido fluindo através de um tubo de seção. 5. Fluxo constante: a velocidade em qualquer ponto é constante no tempo. A velocidade de sucessivas partículas que ocupam um ponto nos instantes sucessivos é o mesmo. Essa continuidade no tempo em um ponto pode ser aplicada também ao resto das variáveis que definem o estado do fluido naquele ponto. Exemplo: bombear água através de uma tubulação de fluxo constante. 6. Fluxo instável: quando as condições em um ponto mudam com o tempo, por exemplo, o bombeamento de água em uma tubulação com vazão crescente.
Em fluidos reais, existem forças de resistência quando há deslizamento de algumas camadas sobre outras, o que torna a energia mecânica transformada em calor e, portanto, o fluido é aquecido. A essa resistência oposta pelo fluido, dá-se o nome de viscosidade.
Princípios de Dinâmica dos Fluidos
A dinâmica dos fluidos estuda os fluidos em movimento e é um dos ramos mais complexos da mecânica. Embora cada gota de fluido obedeça às leis do movimento de Newton, as equações que descrevem o movimento do fluido podem ser extremamente complexas.

Fonte: iaroslavbrylov/ 123RF.
Descrição da figura: A imagem apresenta uma fotografia, onde vemos uma mangueira de jardim na cor laranja aberta com fluxo contínuo de água cristalina. Ao fundo, imagem borrada em tons verde e marrom, representando a natureza.
Em muitos casos práticos, no entanto, o comportamento do fluido pode ser representado por modelos ideais simples, que permitem uma análise detalhada. Inicialmente, vamos trabalhar com o que chamaremos de fluido ideal, ou seja, um fluido incompressível e que não tem atrito interno ou viscosidade.
é uma suposição razoável para líquidos, mas não para gases. Um gás pode ser tratado como incompressível se seu movimento é tal que as diferenças de pressão que aparecem não são muito grandes.
em um fluido, ele dá origem a tensões de cisalhamento quando duas camadas adjacentes se movem uma em cima da outra ou, ainda, quando o fluido se move por tubos ou encontra um obstáculo.
Em alguns casos, essas tensões são desprezíveis quando comparadas com as forças gravitacionais ou aquelas causadas por diferenças de pressão.
Escoamento invíscido e incompressível
Há confusão na literatura mecânica dos fluidos sobre a palavra invíscido e a expressão “fluxo invíscido”. O significado aparente de invíscido não é viscoso. Portanto, o fluxo invíscido parece referir-se ao fluxo de um fluido sem viscosidade. No entanto, não é isso que se entende por fluxo invíscido! Todos os fluidos de importância para a engenharia têm viscosidade, independentemente do campo de fluxo. Os autores que usam a expressão “fluxo invíscido” referem-se ao fluxo de um fluido viscoso em uma região do fluxo, onde as forças viscosas são desprezíveis em comparação com a pressão e/ou forças inerciais. Alguns estudiosos usam a expressão “fluxo sem atrito” como sinônimo de fluxo invíscido. Isso acarreta mais confusão, pois mesmo em regiões do escoamento, onde as forças viscosas líquidas são desprezíveis, apesar do atrito atuar em elementos fluidos, pode, no entanto, haver tensões viscosas significativas. Só que esses esforços se anulam, o que não deixa uma força viscosa líquida significativa em elementos fluidos. Pode-se mostrar que nessas regiões também há uma dissipação viscosa significativa, onde os elementos do fluido, em uma região irrotacional de fluxo, também têm forças viscosas líquidas desprezíveis, não porque neles o atrito não existe, mas porque as tensões de atrito (viscosas) se cancelam. Assim, também podemos encontrar as expressões “regiões invisíveis de fluxo” ou “regiões de fluxo com forças viscosas líquidas desprezíveis”.
Vamos retornar à noção idealizada do escoamento sem atrito denominado escoamento não viscoso ou escoamento invíscido. Ele engloba a maior parte da aerodinâmica e, entre outras coisas, explica, por exemplo, porque aeronaves subsônicas e supersônicas possuem diferentes formas, como uma asa gera sustentação, e assim por diante(...). Usamos a teoria do escoamento invíscido para obter resultados que necessitam de arrasto zero (FOX, 2014, p. 64).
Independentemente da terminologia usada, se as forças viscosas líquidas forem muito pequenas em comparação com as forças de inércia e/ou pressão, as regiões invíscidas de fluxo são regiões de altos números de Reynolds.
Equação da continuidade — vazão
Segundo Çengel e Boles (2015, p. 316), “uma importante área de aplicação da mecânica dos fluidos é a determinação da vazão dos fluidos, e inúmeros dispositivos foram desenvolvidos ao longo dos anos com a finalidade de medir o escoamento”.
Estamos familiarizados com inúmeras leis de conservação, como as leis de conservação de massa, de energia e de momento. Originalmente, essas regras foram aplicadas pela primeira vez a uma quantidade fixa de matéria, chamada de sistema fechado ou apenas sistema e, mais tarde, se espalhou para regiões do espaço chamadas volumes de controle. As relações de conservação também são conhecidas como equações de equilíbrio, uma vez que, qualquer quantidade conservada deve ser equilibrada durante um processo.
A partir do princípio físico que diz que a massa não é criada nem destruída, começamos aplicando um volume de fluido \({{v}_{f}}\), que é expresso dizendo que a massa contida em qualquer volume de fluido não varia com o tempo:
\[\frac{d}{dt}\mathop{\int }_{{{v}_{f}}}^{{}}\rho dV=0\]
Por meio da aplicação do teorema do transporte de Reynolds, encontramos a seguinte expressão geral para conservação de massa que se aplica a um volume de controle:
\[\frac{d}{dt}\mathop{\int }_{{{v}_{0}}}^{{}}\rho dV+\mathop{\int }_{{{S}_{0}}}^{{}}\underset{\scriptscriptstyle-}{n}.\underset{\scriptscriptstyle-}{v}\rho dS=0\]
O que nos dá uma expressão da equação de continuidade em forma integral para um volume de controle fixo. Caso o volume de controle fosse uma variável \({{V}_{C}}\), com o tempo, a expressão obtida seria:
\[\frac{d}{dt}\mathop{\int }_{{{v}_{C}}}^{{}}\rho dV+\mathop{\int }_{{{S}_{C}}}^{{}}\underset{\scriptscriptstyle-}{n}.\left( \underset{\scriptscriptstyle-}{v}-\underline{{{v}_{C}}} \right)\rho dS=0\]
Essa é a equação de continuidade, que é a expressão do princípio de conservação da massa líquida (na ausência de molas e de sumidouros) ⇒ o fluxo de massa, através de uma superfície fechada S, deve ser igual à diminuição, por unidade de tempo, da massa de fluido contida em seu interior.
A equação da continuidade indica que a soma da taxa de variação da massa dentro do volume de controle com a taxa líquida de fluxo de massa através da superfície de controle é zero. A equação da conservação da massa é também chamada de equação da continuidade. Em outras palavras, a taxa de aumento da massa no volume de controle é decorrente do fluxo líquido de entrada de massa (FOX; MCDONALD; PRITCHARD, 2014, p. 145).
Vamos formalizar esse fato em uma equação para a qual temos que definir o fluxo de fluido em uma superfície.
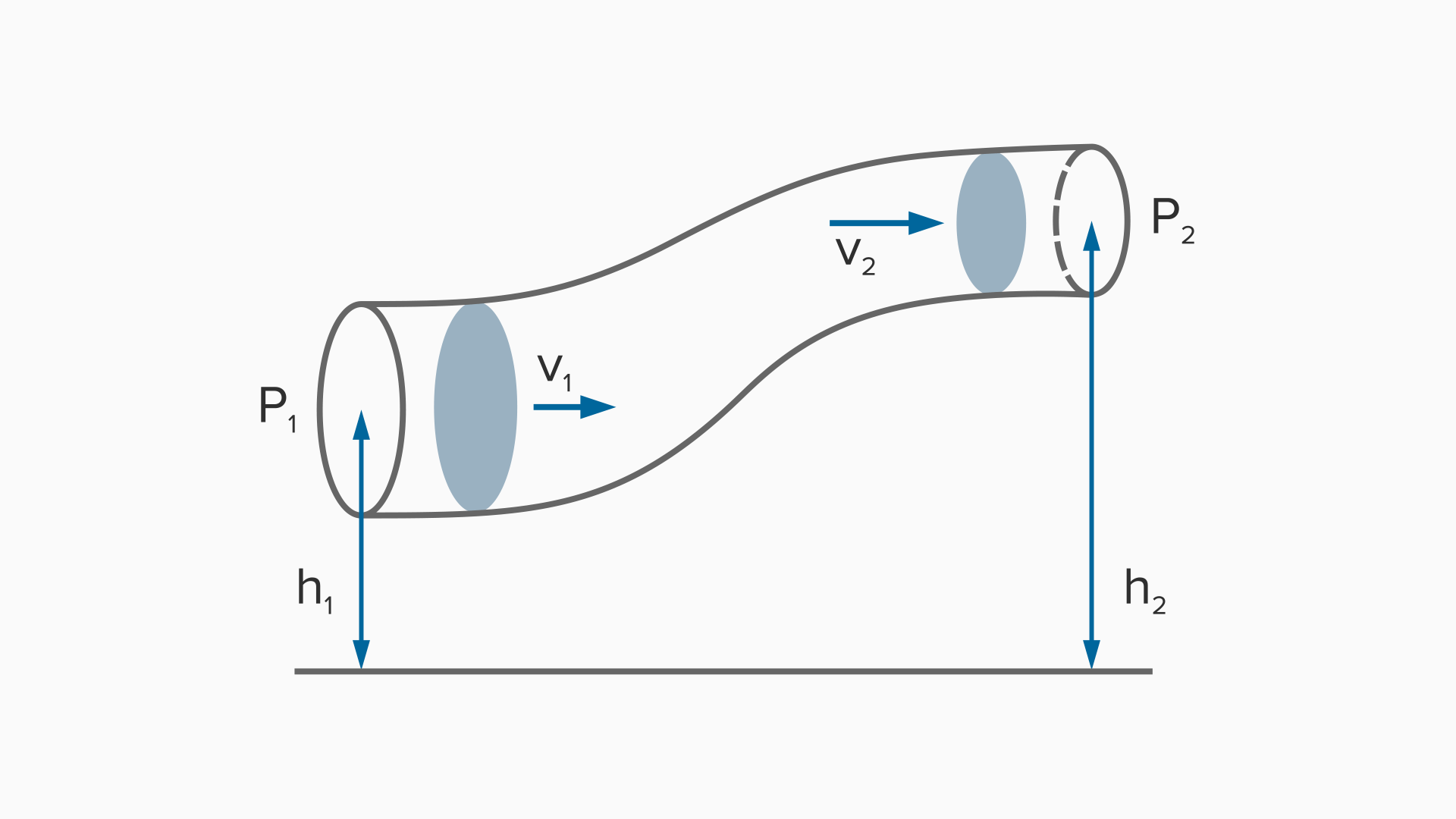
Seja um tubo de corrente em regime de fluxo estacionário, podemos aplicar a equação acima de continuidade a uma parte do tubo compreendido entre duas seções perpendiculares \({{S}_{1}}\) e \({{S}_{2}}\). Como através das superfícies laterais não há fluxo (porque por definição, em cada ponto dele, a velocidade é tangente a elas), podemos expressar que:
\[\mathop{\oint }_{S}^{{}}\rho \underset{\scriptscriptstyle-}{v}.d\underset{\scriptscriptstyle-}{S}=-{{\rho }_{1}}{{v}_{1}}{{S}_{1}}+{{\rho }_{2}}{{v}_{2}}{{S}_{2}}=0{{\Rightarrow }^{{}}}{{\rho }_{1}}{{S}_{1}}{{v}_{1}}={{\rho }_{2}}{{S}_{2}}{{v}_{2}}^{{}}\]
Se, além disso, o fluido é incompressível \(\rho =cte\):
\[{{S}_{1}}{{v}_{1}}={{S}_{2}}{{v}_{2}}\]
expressa a constância do fluxo volumétrico ou a vazão através das seções retas do tubo de corrente ⇒ se a seção do tubo diminui, então, você tem que aumentar a velocidade (mangueira de jardim).